Der dänische Astronom Tycho Brahe besass auf der Insel Hven zwei grosse Observatorien mit einer für die damalige Zeit optimalen Ausstattung. Im späten 16. Jahrhundert erreichte er die Grenze des für das blosse Auge möglichen Auflösungsvermögen von ca. einer Bogenminute(!). Dabei liess er Instrumente herstellen, deren Dimensionen so gross waren, dass die Messskalen sehr fein unterteilt werden konnten. Am berühmtesten ist sein grosser Mauerquadrant (siehe Abb. links).
Johannes Kepler hatte als einer der Ersten klar und richtig erkannt, dass es Naturgesetze gibt, die in mathematischer Form beschreibbar sind und dass diese mathematisch formulierten Naturgesetze uns die Möglichkeit geben, Vorgänge am Himmel zu berechnen. Kepler hat mit Hilfe der Mathematik und der Überzeugung, dass sich die Naturgesetze im Laufe der Jahrtausende nicht verändern und an jedem Ort des Universums die selben sind, die Planetenbewegungen mathematisch untersucht. Er übernahm nach Tychos Tod dessen Beobachtungsmaterial und konnte daraus nach langwierigen Versuchen (20 Jahre) ableiten, dass die Bahnkurve des Planeten Mars (und damit wohl auch der andern Planeten) Ellipsen sind (Sonne im einen Brennpunkt). 2. Keplersches Gesetz
Dieses besagt:Der Radius-Vektor Sonne - Planet überstreicht in gleichen Zeiten gleiche Flächen. In Sonnennähe bewegt sich also ein Planet schneller, als in Sonnenferne, was qualitativ durch jeweilige Richtung und Stärke der Anziehungskraft der Sonne (Betrag entfernungsabhängig) auf den Planeten leicht verständlich ist:
Interessant: Das 2. Keplersche Gesetz erfüllt den Drehmomentssatz, aber auch das Newtonsche Gravitationsgesetz und die Beziehung F = m * a.
3. Keplersches Gesetz
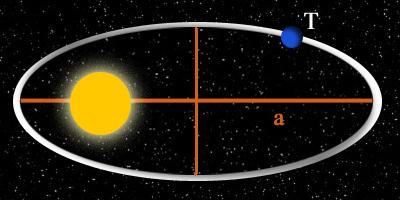Viel später fand er auch noch die Beziehung: Für alle Planeten, die um das gleiche Zentralgestirn kreisen, haben die Quotienten aus dem Quadrat der Umlaufzeit T und der dritten Potenz der großen Bahnhalbachse a den selben Wert C (C = Keplersche Konstante)
(Umlaufszeiten)2 /(Grosse Halbachsen)3 = konstant (also für alle Planeten gleich).
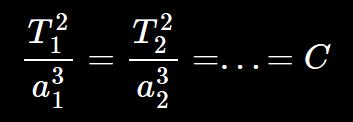Die Indizes [1] und [2] beziehen sich auf 2 Planeten (Planet 1 und Planet 2).Philosophische Betrachtungen Keplers:
"Die Geometrie ist einzig und ewig, ein Widerschein aus dem Geiste Gottes. Dass die Menschen an ihr teilhaben, ist mit eine Ursache dafür, dass der Mensch ein Ebenbild Gottes ist."– Dissertatio cum Nuntio Siderio
ExkursKepler und das Phaenomen Stern von Bethlehem.
Kepler gab die auch heute noch plausibelste physikalisch-astronomische Erklärung für das Phaenomen Bethlehemstern. Diese Theorie ist heute weltweit Standardprogramm in öffentlichen Vorführungen unzähliger Planetarien.Eine Video-Animation und Genaueres zu dieser Theorie: Link: Die Planeten-Konjunktions-Theorie von Kepler |
Weiter
Eine Ebene nach oben