(Zum Anfang dieser kurzen Astronomie-Geschichte: .../astrogeschichte0.htm)
Parallaxen-Verfahren zur Distanzmessung im Kosmos
Die Grundidee am Beispiel Entfernung Erde - Mars
Voraussetzung:
Der Abstand Erde - Mars ist sehr klein gegenüber dem Abstand Mars - Fixsternhimmel und damit 'sehen' Erde und Mars einen 'identischen' Fixsternhimmel.
Durchführung:
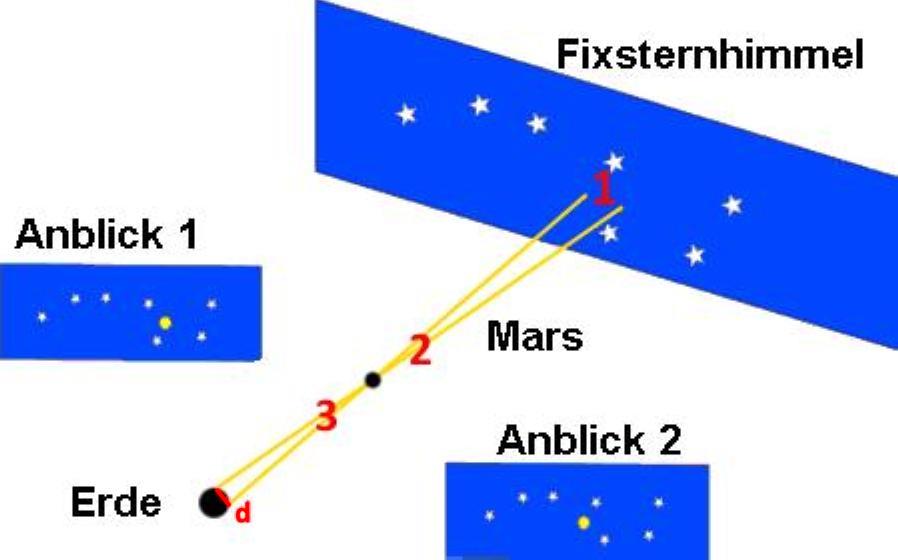
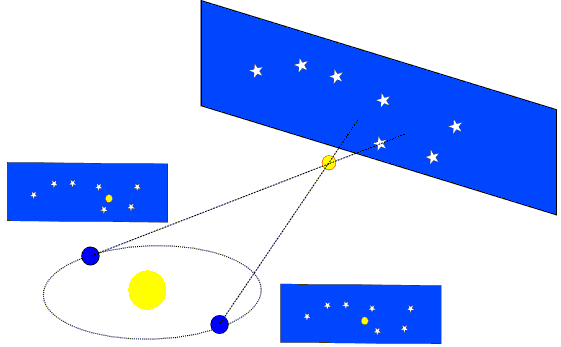
- Der Mars wird gleichzeitig von zwei Orten der Erde mit gegenseitigem Abstand d vor dem Hintergrund des Fixsternenhimmels betrachtet. Am Fixsternhimmel steht Mars scheinbar nicht am gleichen Ort (siehe auch 'Anblick 1' und 'Anblick 2').
- Da man die Winkel-Abstände der Fixsterne an der Himmelskugel natürlich kennt (und diese nach Voraussetzung von der Erde und vom Mars aus gleich sind), kann der Betrag des Winkels 2 für die Verschiebung bei 1 auch von der Erde aus gemessen werdenbestimmt werden. Der Schnittwinkel 3 ist gleich gross wie der Winkel 2 (Scheitelwinkel).
- Unter dem Winkel 3 wird der Abstand d auf der Erde vom Mars aus gesehen. Damit ist aber das Dreieck 'Mars zur Erde' bestimmt und somit die Distanz Erde - Mars ermittelbar.
Es leuchtet ein, dass die Methode umso genauer ist, je weiter die beiden Beobachter auseinander sind. Für die Distanzen zu den allernächsten Fixsternen muss bereits der Erdbahndurchmesser als Standlinie genommen werden, um noch Parallaxenwinkel von ca. 1 Sekunde zu erhalten:
Die eben erwähnte Distanzmessung mit dem Mars ist aber infolge 'schleifender Schnitte' (viel zu schlanke Dreiecke) recht ungenau. Dies war ein Grund für die im Folgenden beschriebene Vermessung eines Transits der gegenüber uns viel näheren Venus vor der Sonne. So konnte der Abstand Venus - Sonne und damit mit Hilfe des 3. Kepler'schen Gesetzes der gesuchte Marsabstand (und sogar aller übrigen bekannten Planeten ermittelt werden.
James Cook und der Venus-Transit (1769)
Planeten-Umlaufzeiten um die Sonne (in ‚Erdjahren') sind ‚relativ einfach' durch systematisches Beobachten zu ermitteln, nicht aber die absoluten Planetenabstände zur Sonne in ‚Kilometern'.
Das heisst:
Aus dem bereits damals bekannten (und hier vorher erwähnten) 3. Keplerschen Gesetz kann man bei bekannten Umlaufzeiten T der Planeten um die Sonne wenigstens die Verhältnisse der Sonnen-Entfernungen der Planeten bestimmen. Die absoluten Entfernungen (in ‚Kilometern') können so aber noch nicht berechnet werden. So wusste man schon früh, dass die Entfernung der Venus von der Sonne das 0,723-fache des Abstandes, also 0,73-mal den Abstand zwischen Sonne und Erde, beträgt, konnte aber keine absolute Entfernungsangabe in Kilometern geben.
'Kilometer-Ermittlungen' wurde von vielen Astronomen in zahlreichen Expeditionen versucht. Besonders berühmt ist jene von James Cook durch Beobachtung und Auswertung eines Venus-Transits vor der Sonne anlässlich seiner Seereise von Tahiti [= südlicher Beobachterstandort] aus betrachtet. Die dabei angewandte Methode stammt von Edmon Halley (1716) und arbeitet auch mit der Auswertung von Parallaxen durch Messungen von Transit-Zeitdauern:
Dazu sollten ein Beobachter weit im Norden (hier: Vardø in Norwegen) und ein Beobachter weit im Süden (hier: Tahiti) jeweils den Venus-Transit vor der Sonne beobachten. Aufgrund der unterschiedlichen Position der beiden Beobachter nehmen sie die Venus-Spur auf der Sonne und die Durchlaufs-Zeiten unterschiedlich wahr (siehe Bild links).
Diese in der Praxis sehr schwierigen Messungen wurden von Astronomen auf der Ersten Südseereise (1768–1771) des Kapitäns James Cook durchgeführt. Die Expedition beobachtete den Transit des Planeten Venus vor der Sonnenscheibe (Venustransit vom 3. Juni 1769) von der Insel Tahiti aus. Dieses spektakuläre und kostspielige Projekt hatte die Bestimmung der Entfernung Erde–Sonne und in der Folge auf Grundlage des dritten Kepler-Gesetzes die Berechnung der Bahnradien aller Planeten unseres Sonnensystems ermöglicht.
Der leicht verständliche Grundgedanke dieser sehr komplexen Messung:
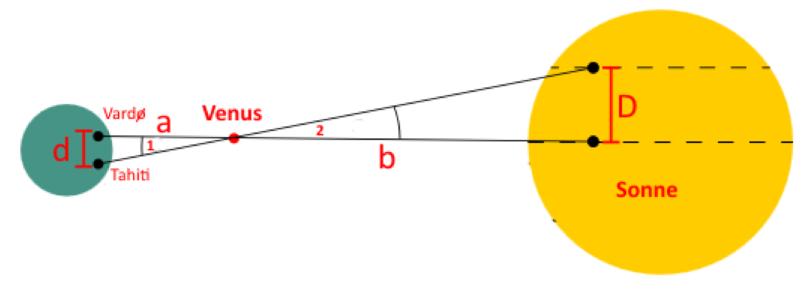Die beiden Dreiecke sind 'ähnlich'. Da d bekannt ist und das Verhältnis
a : b (nach Kepler III) ebenfalls, kann D berechnet werden.
('sehr komplex' bedeutet u.a.:
d und D sind weder parallel noch geradlinig. Das muss rechnerisch auskorrigiert werden.)
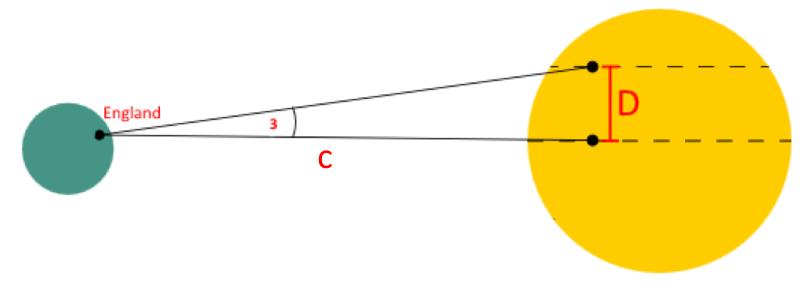Der Winkel 3 kann von der Erde aus ermittelt werden werden (z. B. aus den beiden ermittelten Transit-Zeiten und dem Winkeldurchmesser der Sonne) und da D von vorher bekannt ist, ist das Dreieck bestimmt und c kann berechnet werden. Damit hat man den Abstand Erde - Sonne in Kilometern und damit über das 3. Keplersche Gesetz sämtliche Planetenabstände zur Sonne auf einen Schlag.
Wichtige himmelsmechanische Begriffe: Siderisch - synodisch:
Der mittlere siderische Tag dauert ca. 23 Stunden, 56 Minuten und entspricht einer geometrisch vollständigen Umdrehung der Erde von 360° um ihre Achse.
Dagegen dauert ein Sonnentag (der bürgerliche Tag) ca. 4 Minuten länger, da sich die Erde bis zur Sonnenkulmination um etwa eine 1/365 Umdrehung weiter drehen muss (um wieder 'zur Sonne zu schauen'), da sie sich auf der Umlaufbahn in der Zwischenzeit auch weiter bewegt hat (siehe Abbildung):
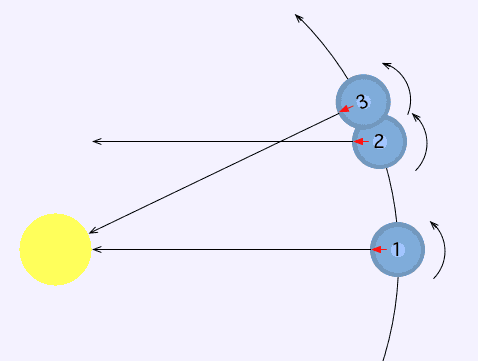
Von 1 nach 2: Siderischer Tag
Von 1 nach 3: Synodischer Tag
Das ist der Grund, dass ein Fixstern jeden Tag 4 Minuten (1440 [min] : 365 [Tage] = ~4 [min/Tag] früher 'aufgeht' oder 'untergeht' bzw. sich der ganze Fixsternhimmel jeden Tag etwas nach Westen 'verschiebt'.
